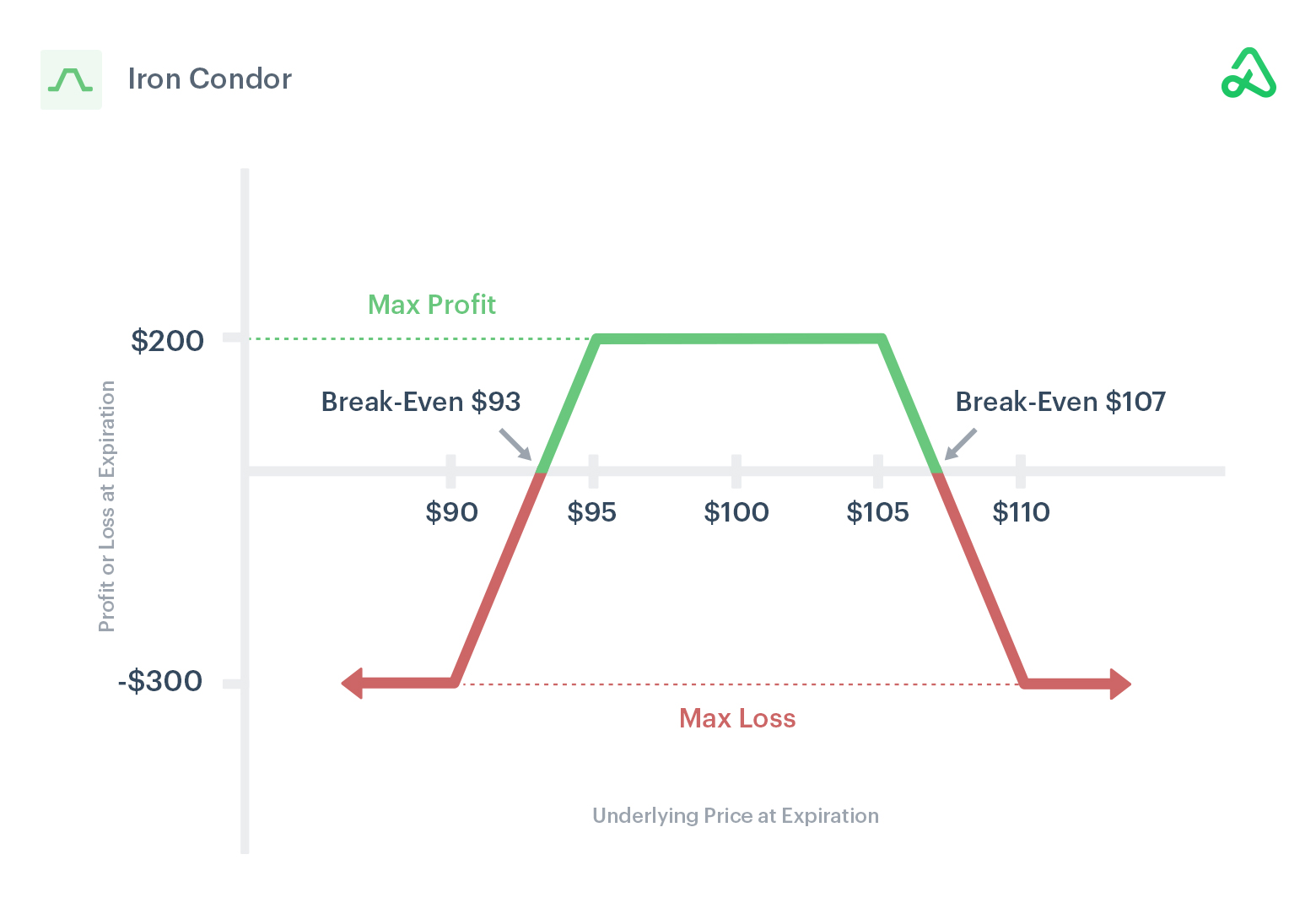
Iron Condor strategy

How to do iron condor effectively using Mathmatical approach

by

Iron condor strategy that offers traders the potential for consistent returns while carefully managing risk. To excel iron condor strategy, it’s essential to harness the power of mathematics. In this article, we’ll delve into the world of Iron Condors and demonstrate how mathematical formulas can be used effectively in this popular trading approach.

Understanding the Iron Condor Strategy

An Iron Condor is a neutral options trading strategy that involves simultaneously selling an out-of-the-money (OTM) call option and an OTM put option while buying a further OTM call and put option. This strategy creates a profit zone within which traders aim to generate returns while carefully controlling risk.

1. Probability Analysis Iron Condor Strategy

One of the cornerstones of Iron Condor trading is probability analysis. This mathematical approach helps traders evaluate the likelihood of success for their trades. Two crucial metrics in this analysis are the Probability of Profit (POP) and the Return on Risk (ROR).

**Probability of Profit (POP):**

The POP calculates the likelihood that the trade will be profitable. It considers the width of the profit zone and the credit received from the trade. The formula for POP is:

\[POP = \frac{Credit Received}{Width of Profit Zone}\]

For example, if you receive a credit of $300 for an Iron Condor with a profit zone width of $700, the POP is:

\[POP = \frac{300}{700} \approx 0.43\]

This means there’s approximately a 43% chance of making a profit in this trade.

**Return on Risk (ROR):**

The ROR measures the potential return relative to the amount of capital at risk in the Iron Condor trade. The formula is:

\[ROR = \frac{Potential Profit}{Maximum Loss}\]

For instance, if the potential profit is $200, and the maximum loss is $800, the ROR is:

\[ROR = \frac{200}{800} = 0.25\]

An ROR of 0.25 implies a potential 25% return on the capital at risk.

2. Delta Management

Delta is a Greek letter used to measure the sensitivity of options to changes in the underlying asset’s price. In Iron Condor trading, maintaining a Delta-neutral position is crucial. This means the combined Delta of the options should be near zero. The formula for Delta is:

\[Delta = \frac{Change in Option Price}{Change in Underlying Asset Price}\]

3. Theta Advantage

Theta, or time decay, plays a significant role in Iron Condor trading. Theta measures how fast the option’s price erodes over time due to time decay. For Iron Condors, time decay works in your favor as you collect premium over time.

The formula for Theta is:

\[Theta = \frac{Change in Option Price}{Change in Time}\]

For example, if your Iron Condor’s Theta is -$20, it means that for each day that passes, your position will increase in value by $20 due to time decay.

Mathematics is a powerful tool in the world of Iron Condor option trading. By applying mathematical formulas, traders can assess the probability of success, manage Delta neutrality, and take advantage of time decay. However, successful trading also requires a deep understanding of market dynamics, risk management, and disciplined execution.

Aspiring Iron Condor traders should embrace the mathematical foundations of this strategy while recognizing that real-world trading involves various variables and risks. By integrating mathematical analysis with sound trading principles, traders can unlock the full potential of Iron Condor option strategies.

Leave a Comment